A gentle introduction to Graph based SLAM

This blog post introduces Simultaneous Localization and Mapping from first principles. It covers necessary topics such as Unimodal Gaussian distributions, Factor Graphs, Matrix Factorization techniques, and the Bayes Tree

Introduction

The problem of Simultaneous Localization and Mapping (SLAM) has a rich history in robotics dating back to 1986 . Briefly, it is the problem of localizing – locating – the robot in an unknown map of the environment, a fundamental problem for any mobile robot. As humans, we unconsciously sense the environment, and build representations in our brains to interact with the environment. To be useful, we would like robots to interact with the environment reliably, which requires accurate SLAM. Robots use sensors to map and localize in the environment, however manmade sensors have tolerances that make the measurements noisy. The key idea in SLAM is to use multiple measurements, and create a consensus estimate about the robot’s location and what the environment may look like.

Since the location of the robot is specified against an unknown map, the localization task takes the form of estimating a piece-wise linear trajectory of the robot, as it moves around in the environment from some arbitrary origin. The map may be represented as a set of distinct landmarks (called landmark-based SLAM) or as a dense representation of the environment such as a voxel map (called dense SLAM).

Recent research (post 2000s) partitions the problem into the frontend and backend.

The front end of a SLAM system deals with pre-processing and associating the raw sensor measurements. This data association results in a set of measurements assigned to each to-be-estimated variable – typically the robot and landmark poses.
The back end is a sensor agnostic optimization framework that takes in the associated measurements and produces the most likely estimate for each variable according to some notion of distance from the actual (unobserved) variable values.

When all the variables to be estimated are Special Euclidean $\text{SE}(n)$ poses, and the sensors generate relative pose measurements between two time instances, the optimization problem is called Pose Graph Optimization (PGO) or Synchronization over the Special Euclidean Group . If all the variables are Special orthogonal $\text{SO}(n)$ rotations, then the problem is also called rotation averaging .

This article addresses the backend optimization and motivates the problem formulation from first principles.

Preliminaries

Filtering vs Smoothing

Most methods prior to 2000s were predominantly filtering methods. In fact, most courses [1] [2] that deal with state estimation also begin the course with topics on filtering techniques.

When a robot moves around in an environment, it’s state space (the variables it estimates) grows. At each time instance, the robot may move, and then make a measurement of its current location. Therefore, internally a new robot pose variable needs to be estimated for the current time step. Loosely speaking, filtering methods only correct estimation errors in the variables at the current time step using only the current measurement, while smoothing methods use the current measurement, and may update its belief about all the variables, past and current. Chapter 3 and 4 of Probabilistic Robotics is a good treatment of Filtering methods relevant to the problem of SLAM.

In this article, I address smoothing techniques.

Gaussian Random Variables

A random variable is an outcome of a random event, and has an associated probability distribution. In our context, the act of measurement is the random event, which outputs a random variable. A classic instance that is cited in many books is an odometry measurement. Due to wheel slip or inconsistent hall-effect, or some other physical property, the sensor measurement may be noisy. In most cases, we expect the sensor to reproduce measurements faithful to its underlying state, but many a time, it may not. This property is mathematically modeled by a Gaussian random variable.

\[\begin{align} \mathbf{z} &= h(\mathbf{x}) + \nu \\ \nu &\sim \mathcal{N}(0, \Sigma) \end{align}\]

Here, equation (1) means that if we knew the state $\mathbf{x}$ then we expect the measurement from the sensor to be transformed by the measurement function $h$. However, since sensors are noisy, the measurement $h(x)$ is corrupted by inherent additive noise $\nu$ in the sensor to produce a measurement $\mathbf{z}$. We model this noise $\nu$ as a random variable sampled from a Gaussian probability distribution. In concrete words, if $h(\mathbf{x})$ were the true underlying measurement, then if we sampled – made multiple measurements – from the sensor, we get noisy measurements with the probability distribution of the noise as follows

\[\begin{align} \nu &\sim \mathbf{z} - h(\mathbf{x}) \\ p(\nu) &= \frac{1}{\sqrt{2 \pi \Sigma}} \exp( \| \nu \|^2_{\Sigma} ) \end{align}\]

Figure 1: The Normal distribution or the Gaussian probability distribution illustrated with different means ($ \mu $) and variances ($ \sigma^2 $). Image taken ingloriously from Wikipedia.

The choice of the probability distribution is rather curious. The Gaussian distribution is part of the exponential family of distributions, and has some convenient algebraic properties:

It is fully described by its sufficient statistic. For instance, even though the Gaussian distribution has probability mass almost everywhere in its domain (infinite support), the distribution is fully described by its mean and covariance.
The product of Gaussian distributions results in another Gaussian distribution i.e., the conjugate prior of a Gaussian distribution is another Gaussian.

Conditional Independence of Random variables

In probability theory, two random variables $\mathbf{x}$ and $\mathbf{y}$ are said to be independent if their joint distribution equals the product of their probabilities. Intuitively, it means that if the value of the random variable $\mathbf{x}$ is observed, then the probability of $\mathbf{y}$ is unaffected:

\[\begin{align} p(\mathbf{x}, \mathbf{y}) = p(\mathbf{x}) p(\mathbf{y}) \end{align}\]

Similarly, if we consider three random variables $\mathbf{x}$, $\mathbf{y}$ and $\mathbf{z}$, then they are said to be conditionally independent, if

\[\begin{align} p(\mathbf{x}, \mathbf{y} | \mathbf{z}) = p(\mathbf{x} | \mathbf{z}) p(\mathbf{y} | \mathbf{z}). \end{align}\]

Conditional independence in the context of SLAM is hopefully illustrated with the following example.

Example 1:

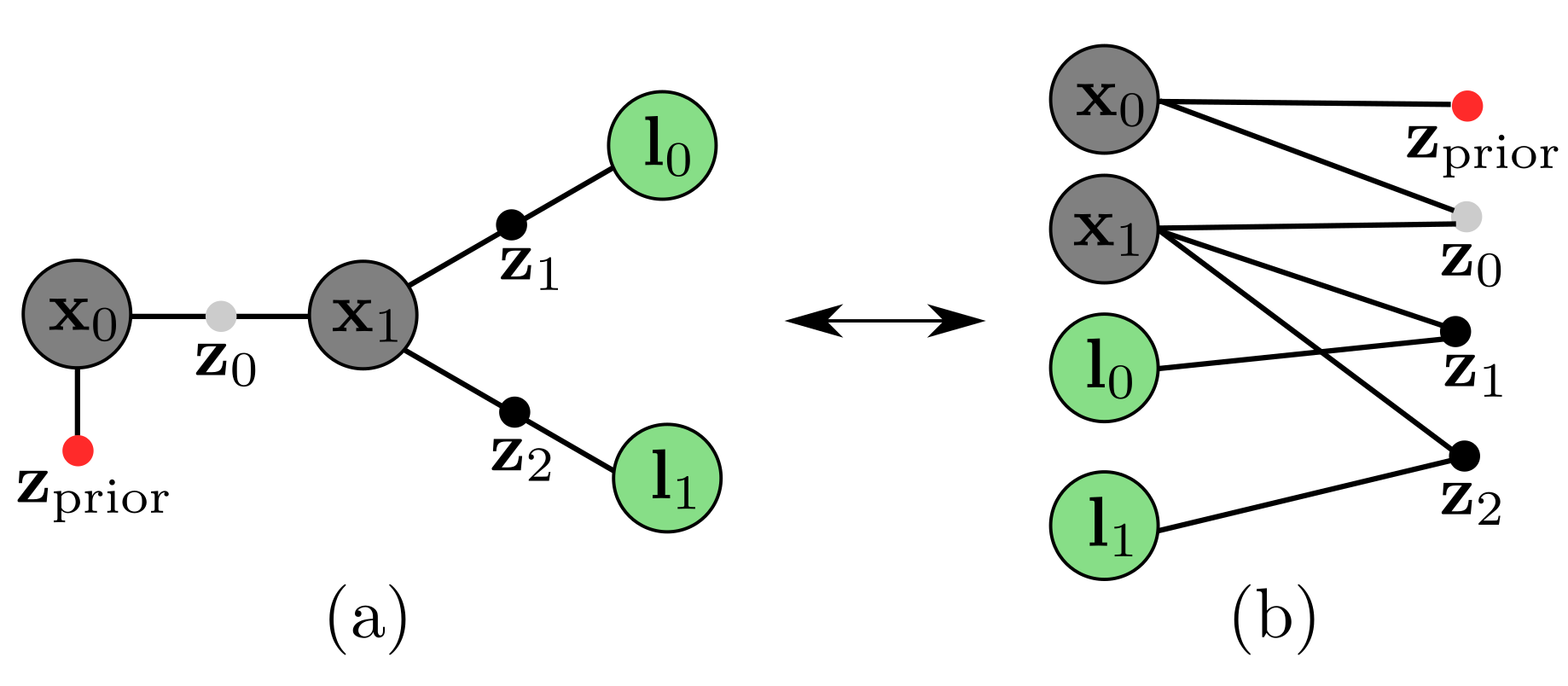
Consider a robot in a one-dimensional world as in Figure 2 (a). At time $t_0$, the robot is at location $\mathbf{x}_0$ and at time $t = 1$ the robot moves to $\mathbf{x}_1$, Now, assume the robot uses its odometry sensor to observe a relative measurement between the two positions, $\mathbf{z}_0$ of (say 50.3 m) as follows

\[\begin{align} \mathbf{z}_0 &\sim h_{\text{odometry}}(\mathbf{x}_0, \mathbf{x}_1) + \nu_{\text{odometry}} \\ p(\mathbf{z}_0 | \mathbf{x}_0, \mathbf{x}_1) &= \mathcal{N}(h_{\text{odometry}}(\mathbf{x}_0, \mathbf{x}_1), \Sigma_{\text{odometry}}) \\ \end{align}\]

Now the robot uses its range sensor – say, a sensor that provides the shortest distance to a particular landmark – to make a measurement $\mathbf{z}_1$ of a landmark $l_0$.

$\begin{align} \mathbf{z}_1 &\sim h_{\text{range}}(\mathbf{x}_1, \mathbf{l}_0) + \nu_{\text{range}}\\ p(\mathbf{z}_1 | \mathbf{x_1}, \mathbf{l}_0) &= \mathcal{N}(h_\text{range}(\mathbf{x}_1, \mathbf{l}_0), \Sigma_{\text{range}}) \end{align}$

Figure 2: Illustration of a 1-D robot that observes two landmarks after moving forward by 50 meters at timestep 1.

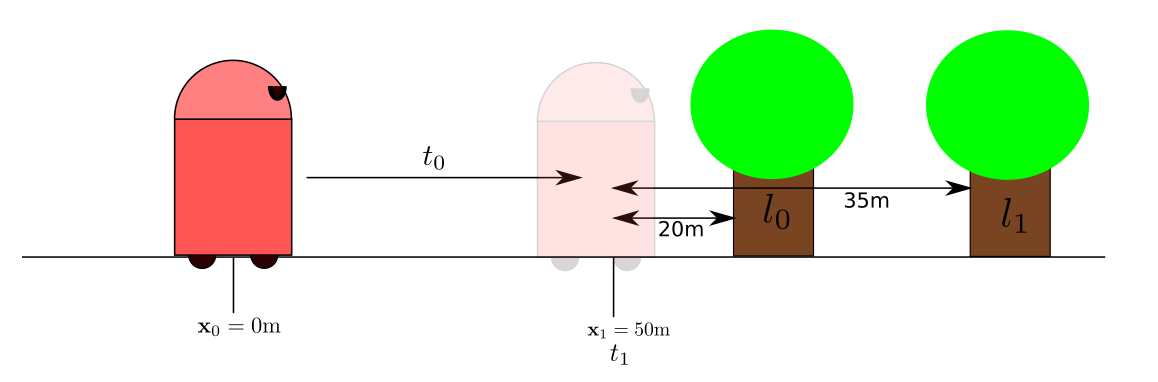
In the above statement, notice, I said that if we are given the state $\mathbf{x}_1$ at time $t = 1$ as 50 meters, then the measurements $\mathbf{z}_1$ and $\mathbf{z}_2$ only depend on $\mathbf{x}_1$, $\mathbf{l}_0$ and $\mathbf{x}_1$, $\mathbf{l}_1$ respectively. If $\mathbf{x}_1$ were not known, then making measurement $\mathbf{z}_1$ would depend on $\mathbf{x}_0, \mathbf{z}_0$ as well as $\mathbf{x}_1, \mathbf{l}_0$.

\[\begin{align} p(\mathbf{z}_0, \mathbf{z}_1, \mathbf{x}_0, \mathbf{l}_0 | \mathbf{x}_1) = p(\mathbf{z}_0 | \mathbf{x}_1) p(\mathbf{z}_1 | \mathbf{x}_1) \end{align}\]

Figure 3(a) is a graphical representation of the above robot, where the state variables are denoted with large circles annotated with variable names, and measurements are denoted with edges with a filled dot.

Next, consider the selected portion – in dotted lines – of Figure 3(a) for simplicity. Here we see that, to sample measurements $\mathbf{z}_0$ and $\mathbf{z}_1$, we need to sample from the joint probability distribution i.e., $p(\mathbf{z}_0, \mathbf{z}_1, \mathbf{x}_0, \mathbf{x}_1, \mathbf{l}_0)$.

\[p(\mathbf{z}_0, \mathbf{z}_1, \mathbf{x}_0, \mathbf{x}_1, \mathbf{l}_0) = p(\mathbf{z}_0, \mathbf{z}_1 | \mathbf{x}_0, \mathbf{x}_1, \mathbf{l}_0) p(\mathbf{x}_0, \mathbf{x}_1, \mathbf{l}_0) \\\]

Now consider the conditional distribution over the two measurements $\mathbf{z}_0, \mathbf{z}_1$. From Equation (6) and (7) we know $\mathbf{z}_0$ only depends on $\mathbf{x}_0$ and $\mathbf{x_1}$, and from Equation (8) a similar argument can be made for $\mathbf{z_1}$. Therefore, we can safely assume the following:

\[\begin{align*} p(\mathbf{z}_0, \mathbf{z}_1 | \mathbf{x}_0, \mathbf{x}_1, \mathbf{l}_0) &= p(\mathbf{z}_0 | \mathbf{x}_0, \mathbf{x}_1, \mathbf{l}_0) p(\mathbf{z}_1 | \mathbf{x}_0, \mathbf{x}_1, \mathbf{l}_0)~~~~\text{conditionally independent}\\ p(\mathbf{z}_0, \mathbf{z}_1 | \mathbf{x}_0, \mathbf{x}_1, \mathbf{l}_0) &= p(\mathbf{z}_0 | \mathbf{x}_0, \mathbf{x}_1) p(\mathbf{z}_1 | \mathbf{x}_1, \mathbf{l}_0)~~~~~~~~~~~~~~~\text{conditioned on redundant variables} \end{align*}\]

The above assumption of conditional independence between measurements given state variables is key in reducing the complexity of estimation.

Why Factor Graphs?

Factor graphs are bipartite graphs – graphs containing two types of random variables – that describe the factorization of a probability distribution. Factorizing a joint probability distribution amounts to finding the subsets of random variables that are conditionally independent of each other and therefore be written as a product.

For example 1, Figure 3(a) concisely represented the factorization of the joint probability distribution between all the random variables.