Lie Theory Back to Basics

This blog post introduces Lie Groups and defines important concepts that are needed for state estimation or SLAM. Largely adapted from "A Micro lie-theory for state estimation in Robotics"

Preliminaries

Manifold

A smooth manifold is a curved and differentiable hyper-surface – one with no spikes / edges – that locally resembles a linear space \(\mathbb{R}^n\) embedded in a higher dimensional space.

Examples:

• 3D Vectors \(\in \mathbb{R}^3\) with unit-norm constraint form the spherical manifold \(\mathbb{S}^3\)
• Rotations in the 2D plane \(\in \mathbb{R}^2\) form a circular manifold
• 3D Rotations form a hypersphere (3-sphere) in \(\mathbb{R}^4\)

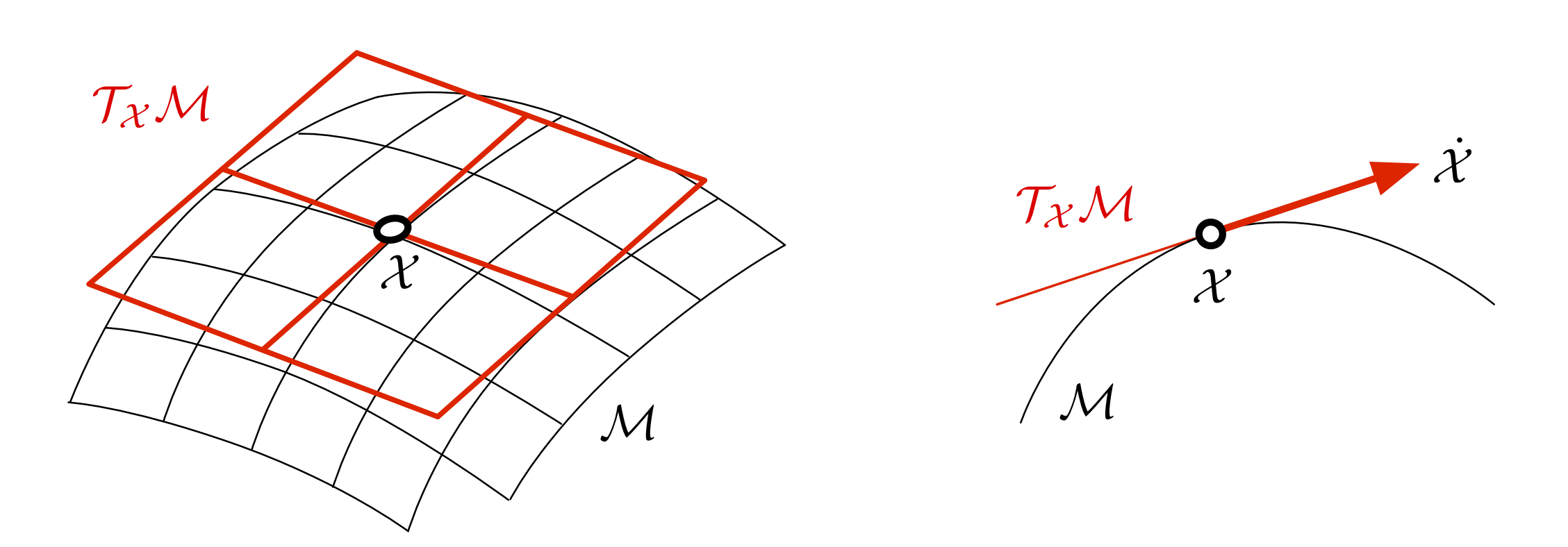
Figure 1: A manifold $$\mathcal{M}$$ and its associated tangent space $$ \mathcal{T}_\times \mathcal{M} (\mathbb{R}^2) $$ tangent at the point $$ \mathcal{X} $$ and a side view. The velocity element $$ \dot{\mathcal{X}} = \frac{\partial{X}}{\partial{t}} $$ does not belong to the manifold but to the tangent space.

Group

A Group \(\mathcal{G}\) is a set with a composition operator \(\circ\), that for elements \(X, Y, Z \in G\) satisfy the following axioms:

1. Closure under \(\circ\): \(X \circ Y \in \mathcal{G}\)
2. Identity \(E\): \(E \circ X = X \circ E = X \in \mathcal{G}\)
3. Inverse \(X^{-1}\): \(X^{-1} \circ X = X \circ X^{-1} = E \in \mathcal{G}\)
4. Associativity: \((X \circ Y) \circ Z = X \circ (Y \circ Z)\)

Notice the omission of commutativity

Lie Group

A smooth manifold that looks identical (example: A sphere, a circle) at every point and satisfies all group properties:

• Composition of Lie group elements remain in the lie group
• Each lie group has an identity element
• Every element has an inverse.

Examples

1. The unit complex number group \(\mathbb{S}^1: z = \cos(\theta) + i \sin(\theta) = e^{i \theta}\) under complex multiplication as the composition operator is a Lie group. A Lie group element \(z \in \mathbb{S}^1\) rotates a regular complex vector \(\mathbf{x} = x + iy\) via complex multiplication to \(\mathbf{x}^\prime = \mathbf{z} \circ \mathbf{x}\). The unit norm constraint of the unit complex group defines a 1-sphere in 2D space.

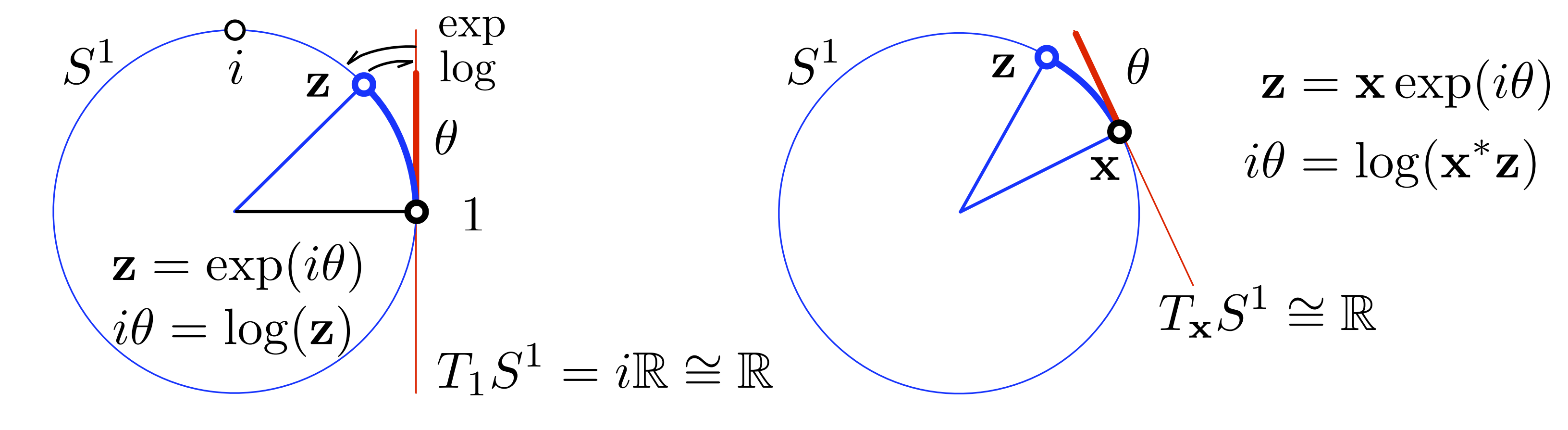
Figure 1: A manifold $$\mathcal{M}$$ and its associated tangent space $$ \mathcal{T}_\times \mathcal{M} (\mathbb{R}^2) $$ tangent at the point $$ \mathcal{X} $$ and a side view. The velocity element $$ \dot{\mathcal{X}} = \frac{\partial{X}}{\partial{t}} $$ does not belong to the manifold but to the tangent space.