Depth Fusion for Large Scale Environments

Implementation of Spatial Hashing in OpenCV RGBD

This project aimed to implement spatial hashing for the TSDF volume data structure in the OpenCV RGBD module, and leverage the same to build a scalable submap based online 3D scene reconstruction system with little to no drift.

TSDF volumes are widely agreed upon in the research community to be locally consistent with minimal drift, therefore a natural mapping model is a PoseGraph[2] of overlapping submaps, each representing a local section of the entire scene. This mapping model allows for periodic global optimization, which corrects accumulating drift retrospectively in the model, as new sensor measurements are incorporated.

The following delineates the pipeline:

Module Pipeline

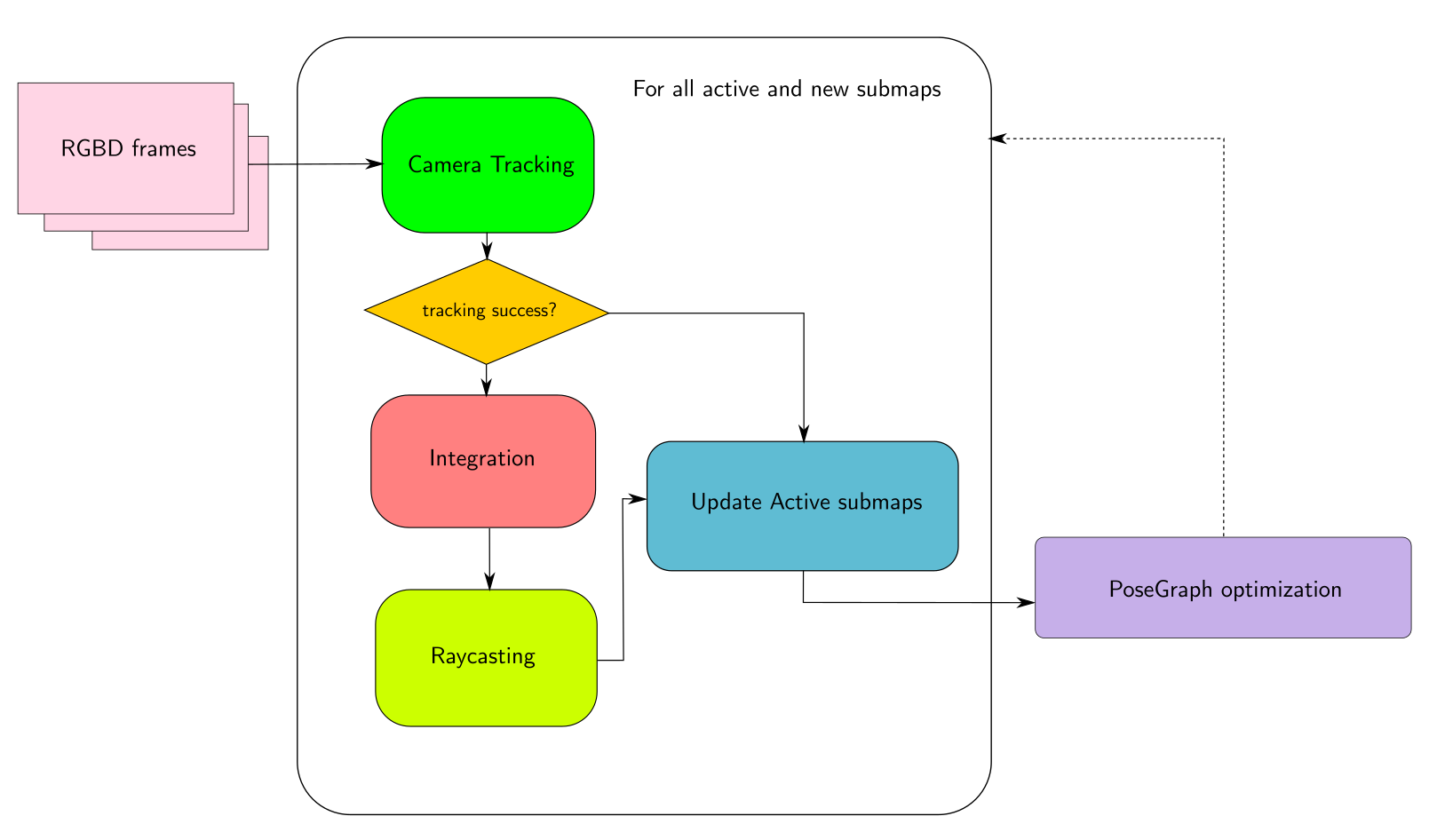
This implementation uses the existing Kinect Fusion[1] pipeline in OpenCV.

Implementation

A sample demo of the application is as shown below, running on the ICL-NUIM dataset:

The implementation in OpenCV contains the following primitives.

Hash-table based TSDF volume

This implementation is based on the seminal work on Voxel hashing. A regular TSDF volume represents a scene as a 3D volume grid of (truncated) signed distance functions. These truncated signed distance functions are simply the shortest distance of each point to its closest surface. While this is simple to implement, this constrains a user to reconstruct scenes of limited size, since the volume size has to be preallocated.

The Hash based volume, stores the volume as an unordered_map of smaller TSDF volume units (volumeUnits), each representing canonically 8³ or 16³ resolution. These volume units are indexed by a 3 dimensional Vector, which is hashed appropriately to minimise the number of hash collisions.

This TSDF volume requires the following important functionalities:

• Integration: During Integration, the TSDF volume automatically allocates new volume units, checking for existing volume units in the current viewing camera frustrum. Integration follows by delegating the task to individual volume units parallely, once the list of volume units to be integrated has been determined.

• Raycasting: Raycasting is required to render the TSDF volume into a virtual image, that is used for tracking. Typically, for each pixel of the to-be generated image, a ray is marched in the volume with fixed steps to obtain an estimated surface distance measurement. In the HashTSDFVolume we get significant performance improvements since we can skip/jump over volume units (typically around 16 voxels length) that are away from the surface.

The following PR provides a CPU implementation of Hash-table TSDF volume in OpenCV:

Submap

The submap class is an abstraction over the hashTSDF volume to support the large_kinfu pipeline. Some questions that are especially relevant with submap based 3D reconstruction are:

• What is the appropriate size of the submap volume?
• When do you terminate and initialize a new submap?
• How do you track and create constraints between multiple submaps in a scene for downstream optimization of poses?

We address question 1. and 2. by using a camera overlap metric, which states that if the current camera frame consistently views - for a threshold number of frames - a new set of volume units that are only allocated recently and haven’t been part of the older frames, then it means that the camera must have moved to a new part of the scene.[4] Once a new submap is instantiated, we initialize it with a submap \(SE(3)\) pose of the frame at which it was created.

We maintain a list of active submaps, all of which are simultaneously tracked at each time-step. The simultaneous tracking provides us with a camera pose w.r.t each submap as \(\mathbf{T}^t_{s_i c}\) where \(s_i\) represents the \(i^{th}\) submap coordinate frame, \(c\) represents the camera coordinate frame and \(t\) represents the current time-step. The relative constraint at each time-step between submap \(s_j\) and \(s_i\) can be obtained as:

\[\mathbf{T}^t_{s_j s_i} = {\mathbf{T}^t_{s_i c}}^{-1} \circ \mathbf{T}^t_{s_j c}\]

A robust estimate of the constraints between submaps over multiple timesteps is then obtained using a simple implementation of Iteratively Reweighted Least Squares (IRLS), which eliminates outlier constraint estimates using the Huber norm.

PoseGraph optimization

Once we have a scene containing dynamically created submaps, we are required to optimize the submap poses to eliminate accumulating camera tracking drift and improved reconstruction

We implement a simple PoseGraph class, and implement second order optimization methods such as Gauss Newton, and Levenberg Marquardt.

The idea here is to abstract the submaps as nodes of 3D \(SE(3)\) poses, and to use the sensor measurements i.e., the robust Pose Constraints between submaps, as obtained from the previous section to correct the pose estimates. For a given submap pair \(s_j\) and \(s_i\) with an existing pose constraint \(\hat{\mathbf{T}}_{s_j s_i}\), we formulate an error metric (factor) as follows:

\[r = \hat{\mathbf{T}}_{s_j s_i} \ominus (\mathbf{T}_{s_i c} \ominus \mathbf{T}_{s_j c})\]

Where \(\ominus\) denotes the \(SE(3)\) right composition i.e., \(\mathbf{A} \ominus \mathbf{B} \triangleq \text{Log}(\mathbf{B}^{-1} \circ \mathbf{A})\)

We minimize the residual rr by linearizing the function and then solving the linear system of equations using a Cholesky solver or a QR solver. (We leverage Eigen library for the linear system solver).

NOTE: Currently, the implementation of Levenberg Marquardt is unstable, and thus for the time being Ceres library is used for the same. However, we will refine the implementation of the optimizer to make the module dependency-free in the future.

The following Pull Request implements the Submap and PoseGraph optimization:

Extensions and Future Work

A large omission in this work is the Relocalization module that is imperative to prevent spurious creation of submaps when the camera revisits previously created submap sections. I plan to add this extension after GSoC.

Typically relocalization modules are implemented using Fast Bag of Words or Dynamic Bag of Words (FBoW, DBoW2/3) methods, which maintain a vocabulary of distinct keyframes as bag of words which can be quickly queried during tracking to detect cases of loop closure and can be used for camera relocalization if tracking fails.

Acknowledgements

It has been very pleasant working with my mentor Rostislav Vasilikhin, (and with Mihai Bujanca), who was enthusiastic and forthcoming with all the issues during the 3 months of Google Summer of Code. It was especially rewarding and pedagogic implementing modules that form the basis of most Dense SLAM systems today, and the added benefit of making a significant open-source contribution in the process has made summer of 2020 worthwhile and interesting.

I would like to thank Google for giving me this opportunity as well!